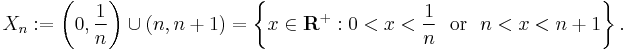Interlocking interval topology

Not to be confused with Overlapping interval topology.

In mathematics, and especially general topology, the interlocking interval topology is an example of a topology on the set S := R+ \ Z+, i.e. the set of all positive real numbers that are not positive whole numbers.[1] To give the set S a topology means to say which subsets of S are "open", and to do so in a way that the following axioms are met:[2]

  1. The union of open sets is an open set.
  2. The finite intersection of open sets is an open set.
  3. S and the empty set ∅ are open sets.

Construction

The open sets in this topology are taken to be the whole set S, the empty set ∅, and the sets generated by

X_n�:= \left(0,\frac{1}{n}\right) \cup (n,n%2B1) = \left\{ x \in {\bold R}^%2B�: 0 < x < \frac{1}{n} \ \text{ or } \ n < x < n%2B1 \right\}.

The sets generated by Xn will be formed by all possible unions of finite intersections of the Xn.[3]

References

  1. ^ Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, pp. 77 – 78, ISBN 048668735X 
  2. ^ Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, p. 3, ISBN 048668735X 
  3. ^ Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, p. 4, ISBN 048668735X